For most of the month of June I gathered photometric data for the star OV Boötis (OV Boo), an eclipsing cataclysmic variable star with a very short orbital period. The data were acquired using the #2 16-inch with an SBIG ST8xme camera and clear filter. The images were calibrated using BHO_ImageCalibration, and reduced using the PPX photometry program. With the exception of the first night of observing, the exposure time for each image was 50 seconds. Peranso period-search software was used to determine an orbital period of 3996.7 ± 1.4 seconds.
OV Boötis
Like all cataclysmic variable (CV) stars, OV Boo is a double star system in which a collapsed (white dwarf) star is siphoning material from the outer atmosphere of it’s companion star, a low-mass red dwarf that is over filling it’s Roche lobe. There are, however, some unique features to this star. First of all, its orbital period is shorter than any other hydrogen-rich CV. There are reasonably well understood reasons why the orbital period of a “normal” CV cannot be less than about 78 minutes. Observations back up that limit; the only CVs with shorter periods are helium-rich stars. That is, until OV Boo was discoverd. OV Boo’s orbital period is 66.6 minutes, a full 12-minutes shorter than is though possible. It is also the CV with the fastest proper motion. Finally, spectra of the red dwarf star show it to be “metal” poor. These last two points indicate that it is likely a population-II object, the only one among the 3000 or so known CVs.
One of the consequences of being a population-II (older, early generation) star is that their atmospheres lack the quantity of “metals” (elements heavier than Helium) found in population-I (younger, more recent generation) stars. As a result, the atmospheres of population-II stars have much lower opacity. You can think of opacity in this sense as resistance to energy escaping. Because the atmospheres of population-II stars are more transparent they tend not to “bloat up” as much as their younger cousins and so tend to be a bit smaller for a given mass. There is a strong correlation between the orbital period of a CV and the mean density of the secondary star such that:
where “P” is the orbital period and is the secondary star’s mean density. So we can understand why OV Boo has such a short orbital period; its secondary is smaller, thus more dense, than the population-I stars that typically are found as secondaries in CVs.
OV Boo has been the subject of a number of investigations which indicated it was similar in many ways to WZ Sge, another short orbital period CV (82 min) that has a very low mass transfer rate and only outbursts very infrequently. In fact, in March of this year, OV Boo was observed in outburst for the very first time. Subsequent observations by the Center for Backyard Astrophysics (CBA) detected what are called “superhumps” in its early outburst phase, confirming its membership in the WZ Sge class.
Better Late than Never?
As often happens, I was not able to participate in the CBA campaign to monitor OV Boo’s outburst, due to a combination of lousy weather and being very busy running and, ultimately, selling my business (Orion Studios). Still, I wanted to see if I could nail down the orbital period. Doing so would require the deepest photometry I’ve yet attempted from BHO as the eclipses take OV Boo’s brightness to as low as 19th magnitude. That’s a tall order for a small telescope anywhere, let alone from the middle of a major city with its god-awful light pollution. The challenge was made all the more difficult because the eclipses themselves are very fast. That meant I could not take long exposures which might improve the signal-to-noise ratio of the resulting photometry. Instead, I had to stick to shorter exposures which limited the precision of my measurements to around 0.05 magnitudes.
Observations of OV Boo - June 2017
| Date | Number of Images | Number of Eclipses |
|---|---|---|
| 2017 June 01/02 | 100 | 3 |
| 2017 June 02/03 | 195 | 3 |
| 2017 June 03/04 | 229 | 3 |
| 2017 June 08/09 | 237 | 3 |
| 2017 June 09/10 | 216 | 3 |
| 2017 June 24/25 | 174 | 3 |
| 2017 June 25/26 | 246 | 4 |
| 2017 June 27/28 | 266 | 5 |
All of the exposures were 50 seconds in duration, except for the first night, where the images were 200 seconds in duration. After that first night I decided to try increasing the sampling cadence as the eclipses were short.
Reductions and Analysis
The images were calibrated using a home-brewed python script called BHO_ImageCalibrate. The script handles all of the usual steps of bias-subtraction, dark-image scaling and subtracting, and flat-fielding. The photometry was performed using PPX, a program written in the IDL language. PPX finds all of the stars in each image and performs matching of stars from one image to the next. PPX then performs variance-weighted optimal-extraction photometry for the comparison stars and the variable star. I used DPlot to produce the chart (shown below) illustrating the photometric results for the night of June 27/28, 2017.

As can be seen in the table of observations, I managed to catch a total of 27 eclipses. The next step was to correct all of the observation times to heliocentric time – the time an observer on the sun would observe a given phenomenon. The heliocentric correction removes the changing arrival time of photons due to the earth’s movement around the sun. In the most extreme cases that time difference can be as much as 19 minutes. The data were then fed to Peranso, which incorporates a number of period-finding algorithms. Just looking at the chart, above, it’s obvious the period is a bit over 0.045 days. I used Peranso’s implementation of the Lomb-Scargle algorithm to determine that the orbital period is seconds.
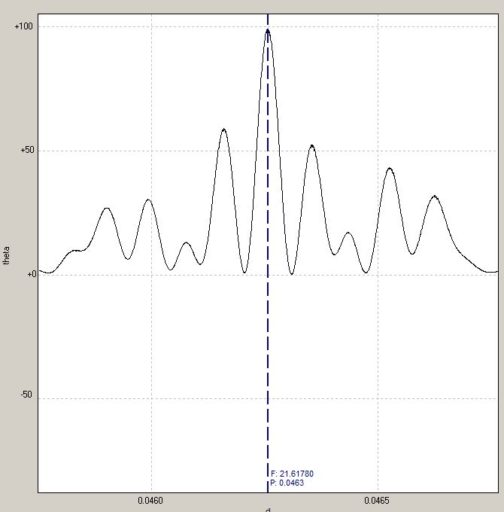
This is the periodogram created by the Lomb-Scargle function in Peranso. Essentially the higher the “significance” ( the y-axis ) the more likely it is that the period is the “correct” one. The dashed vertical line indicates the location of the periodogram’s peak – labeled as F=21.61780 cycles per day, or a period of 0.0463 days.
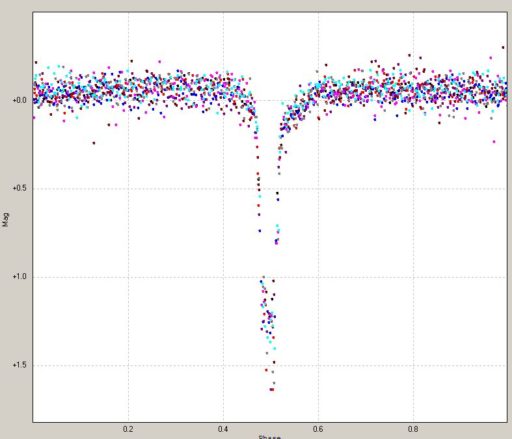
This shows all 1663 measured magnitudes, folded onto a single plot whose x-axis is scaled to one full cycle of 0.0463 days. Note that near central eclipse the data become pretty ratty. Ya – 19th mag object with short exposure times from the city!



Leave a Reply